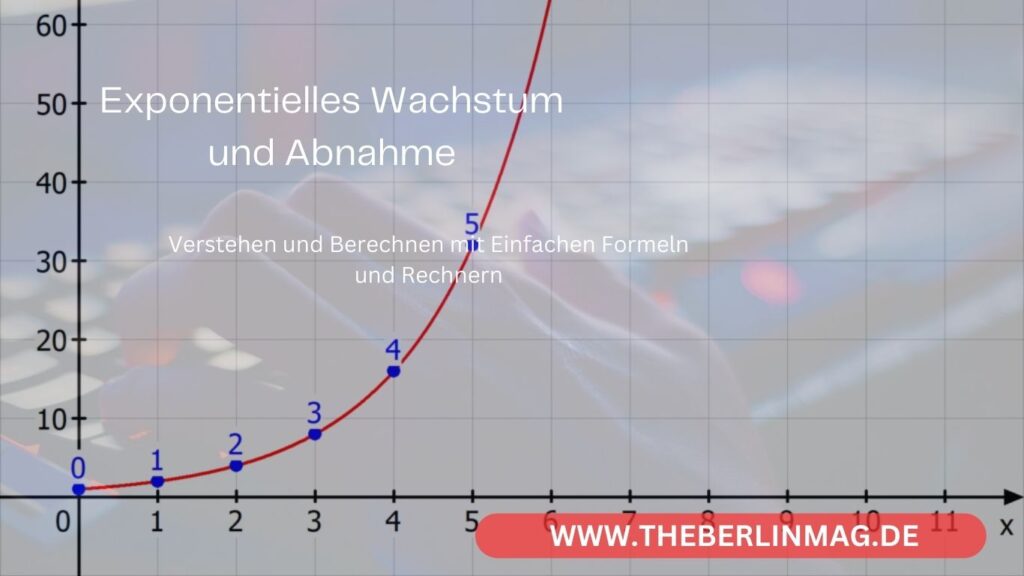
Exponentielles Wachstum und exponentielle Abnahme sind fundamentale Konzepte in der Mathematik und Naturwissenschaft, die vielfältige Anwendungen in Bereichen wie Biologie, Chemie, Physik und Ökonomie finden. Dieser Artikel bietet einen tiefgehenden Einblick in die Welt des exponentiellen Wachstums und der exponentiellen Abnahme, erklärt die zugrundeliegenden Prinzipien, Formeln und Berechnungsmethoden und zeigt anhand von Beispielen, wie diese Konzepte in der realen Welt angewendet werden können.
Was ist Exponentielles Wachstum und Exponentielle Abnahme?
Exponentielles Wachstum und exponentielle Abnahme beschreiben Prozesse, bei denen die Änderungsrate eines Wertes proportional zu seinem aktuellen Wert ist. Beim exponentiellen Wachstum nimmt der Wert über die Zeit exponentiell zu, während er bei exponentieller Abnahme exponentiell abnimmt. Diese Prozesse werden durch die Exponentialfunktion modelliert, die als Wert = Anfangswert * e^(Wachstumsrate * t) dargestellt wird, wobei e die Basis des natürlichen Logarithmus und t die Zeit darstellt.
Die Exponentialfunktion: Grundlagen und Eigenschaften
Die Exponentialfunktion, oftmals als f(t) = a * e^(kt) geschrieben, ist die mathematische Grundlage des exponentiellen Wachstums und der exponentiellen Abnahme. Hierbei steht a für den Anfangswert, e für die Basis des natürlichen Logarithmus, k für die Wachstums- oder Abnahmerate und t für die Zeit. Diese Funktion zeichnet sich durch ihr charakteristisches exponentielles Wachstum oder Zerfall aus.
Berechnung des Exponentiellen Wachstums: Formeln und Beispiele
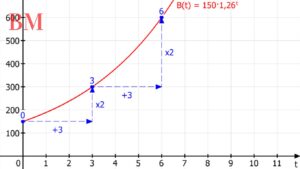
Um exponentielles Wachstum zu berechnen, verwendet man die Formel Wert = Anfangswert * e^(Wachstumsrate * t). Diese Formel ermöglicht es, den zukünftigen Wert einer Größe zu berechnen, die exponentiell wächst. Beispiele hierfür könnten die Wachstumsrate einer Bakterienkultur oder die Zunahme einer Bevölkerung sein.
Der Rechner für Exponentielles Wachstum: Wie und Warum?
Ein Rechner für exponentielles Wachstum erleichtert die Berechnung komplexer exponentieller Wachstumsprozesse. Durch die Eingabe von Anfangswert, Wachstumsrate und Zeit kann der zukünftige Wert schnell und genau ermittelt werden. Solche Rechner sind besonders nützlich in der Wissenschaft und in der Finanzwelt.
Lesen Sie auch: Sons Of The Forest Xbox Series X
Exponentieller Zerfall: Ein Einfaches Erklärungsmodell
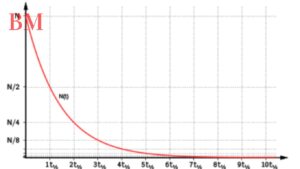
Exponentieller Zerfall ist das Gegenstück zum exponentiellen Wachstum und beschreibt Prozesse, bei denen eine Größe über die Zeit exponentiell abnimmt. Ein klassisches Beispiel ist der radioaktive Zerfall, bei dem die Menge eines radioaktiven Stoffes über die Zeit exponentiell abnimmt.
Die Wachstumsrate bei Exponentiellem Wachstum Bestimmen
Die Wachstumsrate ist ein Schlüsselfaktor beim exponentiellen Wachstum. Sie bestimmt, wie schnell eine Größe zunimmt. Die Bestimmung der Wachstumsrate ist essentiell für das Verständnis und die Vorhersage von Wachstumsprozessen.
Verdopplungszeit und Halbwertszeit: Berechnung und Bedeutung
Verdopplungszeit und Halbwertszeit sind wichtige Konzepte beim exponentiellen Wachstum und Zerfall. Die Verdopplungszeit gibt an, wie lange es dauert, bis eine Größe sich verdoppelt, während die Halbwertszeit angibt, wie lange es dauert, bis die Hälfte einer Größe zerfallen ist.
Anwendungsbereiche des Exponentiellen Wachstums
Exponentielles Wachstum findet Anwendung in vielen Bereichen, von der Biologie (z.B. Wachstum von Bakterienkulturen) über die Ökonomie (z.B. Zinseszins) bis hin zur Technologie (z.B. Wachstum von Computertechnologien).
Graphische Darstellungen: Exponentielles Wachstum Visualisieren
Graphische Darstellungen sind ein mächtiges Werkzeug, um exponentielles Wachstum und exponentiellen Zerfall zu visualisieren. Sie helfen, die Dynamik dieser Prozesse zu verstehen und zu veranschaulichen.
Lesen Sie auch: Switch Lite An TV Anschließen
Vergleich: Exponentielles vs. Lineares Wachstum
Im Vergleich zum linearen Wachstum, bei dem die Wachstumsrate konstant bleibt, zeichnet sich exponentielles Wachstum durch eine Wachstumsrate aus, die proportional zum aktuellen Wert ist. Dies führt zu einem viel schnelleren Anstieg oder Abfall.
Zusammenfassung
- Exponentielles Wachstum und Abnahme beschreiben Prozesse mit einer Änderungsrate proportional zum aktuellen Wert.
- Die Exponentialfunktion ist die mathematische Basis dieser Phänomene.
- Berechnungen von exponentiellem Wachstum und Zerfall erfordern Verständnis von Formeln und Wachstumsraten.
- Verdopplungs- und Halbwertszeiten sind wichtige Kennzahlen in diesem Kontext.
- Exponentielles Wachstum hat breite Anwendungen in verschiedenen wissenschaftlichen und wirtschaftlichen Bereichen.
- Der Vergleich von exponentiellem und linearem Wachstum zeigt die Dynamik und Potenz von exponentiellen Prozessen.
Weitere aktuelle Nachrichten und Updates finden Sie The Berlin Mag.